Understanding Inko Memory Management Through Data Structures
I briefly described Inko’s unique memory management model in my previous article. In this one, I want to go into a little more detail on single ownership and move semantics by implementing a few linked lists, and a couple graphs. This is a tutorial about Inko and not about data structures, so I am assuming that you have a passing knowledge of the data structures in question (or know how to use a search engine to get that passing knowledge).
These memory management concepts are (mostly) not new; c++ has had them for well over a decade, and Rust has had them pretty much from the beginning. However, they may seem rather foreign if you’re used to a garbage collected language, and this article is intended to introduce them for folks that have never encountered them before.
Consider Multiple Ownership
In those modern languages that feature a run-time garbage collector, you can have as many references to an object as you like, and these references are all treated as equals. The object lives as long as least one of those references exist, and any memory associated with it will automatically be freed up “some time after” the last reference is dropped.
In fact, most such languages don’t use the word ‘reference’ or ‘pointer’ for these constructs. They’re just multiple names for the same object.
Consider this Python code for a moment:
def first(elements: list[str]):
return elements[0]
x = ["some", "strings"]
y = x
print(id(x), first(x))
print(id(x), first(y))
The output varies depending on what id returns for any given run, but it’ll look something like this:
4410450048 some
4410450048 some
In this code, the variables x, y, and elements all refer to the exact same list in memory. There are
not multiple copies of the list, and you can access all three variables whenever they are in scope. Because this is Python,
which uses reference counting and a garbage collector, you can rely on that fact. No matter what order the variables go
out of scope, no matter what other objects you attach the list to, the list will exist at least until the last reference disappears.
This is easy to learn, easy to understand, and eliminates a huge number of potential problems (both in ability to code/understand and in bugs or security holes) that show up in languages that don’t have garbage collectors.
No wonder such languages are extremely popular.
Unfortunately, garbage collection comes with a cost: the memory and CPU cycles that are dedicated to keeping track of all those names and cleaning up the memory when it truly isn’t needed anymore are memory and CPU cycles that can’t be spent on meaningful things.
Ideally, it would be possible to have this ease of coding in such a way that the compiler could know in advance when the memory isn’t needed anymore and insert the code to deal with it at exactly that time, but this is a really hard problem.
So many languages that don’t have a garbage collector are using single ownership instead. Even if the language doesn’t explicitly support single ownership, programmers in those languages have learned that the best way safely operate in those languages is to add a sort of manual single ownership style to their coding process. For example, Evan Ovadia recently wrote an excellent article describing how you might do this in C.
To be clear, you aren’t required to use single ownership in (most of) those languages. Many provide some variation on a reference counted pointer, and you can always implement a garbage collector in any of those languages (or use a third-party garbage collection library) if your use case requires one.
Except Inko. In Inko, Single Ownership is (more or less) your only way of interacting with memory in the application. I was skeptical of this at first, but I’ve implemented some fairly complicated data structures in it to test the theory and I’ve become (almost) convinced that it is a workable approach.
Single Ownership
The idea behind single ownership is that you, the programmer, have to pick one of the many variables to be the “owning” variable. Single = one. How much simpler can it be?
This doesn’t mean you can’t have other variables that refer to that variable (that would be unique ownership, which is actually a thing in Inko and I’ll probably dive into it in a different article). However, any references to that variable are considered subservient to the “owning” variable. They are less powerful.
By itself, single ownership prevents (or at least avoids, depending on the language) so-called “double free” errors, where you try to give the same piece of memory back to the operating system more than once. Because there is exactly one owning variable, the memory is freed exactly when that owning variable goes out of scope.
However, there is another insidious bug that creeps into manually memory-managed programs, called “use after free.” Single ownership by itself doesn’t prevent that. If you have any other (non-owning) references to that variable, you, the programmer, have to be very careful that you don’t do anything with those references after the owning variable has gone out of scope.
Different languages provide different levels of support for this; Rust is the gold standard in that it will tell you at compile time if you made this dumb move. This comes at a cost, however, as the work the Rust compiler has to do to generate the proof that you didn’t mess up is terribly slow.
Inko does it differently. Your code will happily compile if you access a reference after the owned variable it points to goes out of scope. However, instead of introducing a security hole, it will tell you at runtime if you try to access a reference after this happens. The error is generated when you drop the owning variable, rather than when you access the non-owning reference. We’re going to see a lot of it in this code.
Move Semantics Schmoove Semantics
A closely associated concept that is usually taught alongside Single Ownership is move semantics. The idea behind move semantics is that while it’s true that only one variable can own a piece of data, doesn’t always have to be the exact same variable. In other words, you can “move” ownership from one variable to another.
Articles I’ve read always make a big deal out of move semantics, but I don’t know why. They’ll show you an example something like this:
class async Main {
fn async main() {
let hello = ["hello", "world"]
let world = hello
let something = hello # won't build
}
}
The reason this won’t build is that at the time we assigned hello to world, we have “moved” the data out of the hello
variable and into the world variable. You aren’t allowed to access the variable after you move it.
The reason I hate this example is: Nobody ever writes code like this. If you expect a variable to be named “something” or “world”, then name it that to begin with. So let’s just skip that example and write a linked list, ok?
Singly Linked List
Singly Linked lists are simple data structures. Each ’node’ in the list contains some sort of link to the next node in the list. Here’s a very basic example:
class Node {
let @next: Option[Node]
}
class async Main {
fn async main() {
let tail = Node {@next = Option.None}
let head = Node {@next = Option.Some(tail)}
}
}
This manually constructs a linked list with two nodes, a head and a tail, with no links in between.
The important thing to notice is that the @next field in the Node class is an owning field.
No matter how long the chain gets, each link in the chain owns the next link in the chain.
Typically, we put the nodes of a linked list into a wrapping class to hold the data and behaviour:
class Node {
let @next: Option[Node]
}
class pub LinkedList {
let @head: Option[Node]
fn pub static new() -> LinkedList {
LinkedList {
@head = Option.None
}
}
}
class async Main {
fn async main() {
let list = LinkedList.new()
}
}
This is still fairly simple. Each link in the chain still owns its field pointing to the next link in the chain, and each linked list owns the head node, so we can access the entire chain, one link at a time.
This code is missing something, though: data! There’s no point in creating a list for creating a list’s
sake. You need to store something in it. So let’s add a @data field to Node.
Now, Inko is a strongly typed language, which means I need a type for data. I could just make a list of
integers or list of strings or something, but that doesn’t seem like it’ll be too useful. so let’s
turn this into a set of generic classes instead. Start with Node:
class Node[T] {
let @next: Option[Node[T]]
let @data: T
}
This is saying that “we don’t care what type of data the node stored as long as the node that we are pointing to stores the same type of data.”
Note that the node owns it’s @data field. This means that data will be kept in memory as long as the node is kept in memory.
This change alone won’t compile, though, because LinkedList isn’t generic yet. Let’s do that:
class pub LinkedList[T] {
let @head: Option[Node[T]]
fn pub static new() -> LinkedList[T] {
LinkedList {
@head = Option.None
}
}
}
This is saying “we don’t care what type of data we’re storing, so long as the head node stores that type of data,” and since the previous
code says that the next node must store the same type of data, we’re actually asserting that all the data stored in any one list
must be the same type.
Let’s implement the insert method, next. In fact, let’s do it twice!
Inserting into a Linked List (two ways)
There are actually two ways that we can do this:
- The object oriented programming way: We pass the new data into an insert method and update the head of our linked list object to point to a new node. The new node’s
nextnode is the list’s oldhead. - The functional programming way: We move the linked list into a method that returns a new linked list with the new head node, assigning that to the old value.
These are subtly different, and I want to implement both of them for demonstration purposes. We’ll start with the functional programming way because it contains fewer new concepts.
Functional insert (move semantics)
fn pub move move_insert(data: T) -> LinkedList[T] {
match self {
case {@head = old_head} -> LinkedList {
@head = Option.Some(
Node {
@next = old_head,
@data = data
}
)
}
}
}
The first thing to notice here is that this function is returning a new LinkedList. We’re not updating the existing one. In fact, we are moving the old linked list into this
function. That’s what the fn pub move bit means. Well, fn pub actually means “public function”, so it’s just the move part of fn pub move that we’re interested in.
When this function ends, the old linked list will go out of scope and its memory will be freed. That means we have to be sure to move
any interesting bits out of the old linked list or they will be forever lost. Specifically, we’re interested in the old list’s @head field, which needs to become
the @next field on a new node in our new list.
The only way to destructure an existing object in Inko is using the match keyword. It works similar to pattern matching in other languages I’ve used. Inko is an expression oriented
language, so the implicit return value of this function is the return value of the match statement, which is the return value of whichever arm was matched. In this case,
there is only one arm and it’s guaranteed to match, so the return value is the Linked List returned from the only case.
Here’s how you would use this move_insert linked list in practice:
class async Main {
fn async main() {
let mut list = LinkedList.new()
list = list.move_insert("hello")
list = list.move_insert("world")
}
}
Notice that the list variable is assigned as let mut. mut is short for “mutable” and means that we are allowed to assign completely new linked lists to the list
name. Reading this code from top to bottom, we are doing the following:
- Creating a new, empty
LinkedListand assigning it to the mutablelistvariable. - Moving that empty linked list into its
move_insertmethod, which returns a linked list containing a single string,"hello". We assign that new linked list to thelistvariable, which is currently in an undefined state because we moved the value out of it. - Moving that single value linked list into its
move_insertmethod, which returns another new linked list containing two values. Again, we assign the new linked list to thelistvariable which was emptied by the move.
Note that this code will not work:
fn async main() {
let mut list = LinkedList.new()
list.move_insert("hello")
list.move_insert("world")
}
In fact, this is doing the same thing as the example I didn’t like (remember that?), where we tried to access a variable after we moved it. It’s not as obvious as it was in that example, but it is an actual real world bug that you are likely to encounter.
Because we defined move_insert with fn pub move, we are moving the list value into that function. It is returning a brand new list, but we aren’t assigning that list to anything,
so it has already gone out of scope and been cleaned up. The second time we call list.insert, the list variable is no longer meaningful because we moved the data in it on the previous call.
Luckily, Inko protects us from ourselves and gives us a clean error message at compile time:
src/main.inko:36:5 error(moved): 'list' can't be used as it has been moved
This functional style is legitimate Inko. You could write entire programs without references if you wanted to move data into and out of functions like this. However, I think the object oriented style is more common, so let’s look at that next.
Object Oriented Insert (Mutable reference)
Here’s a first stab at a mutating insert function:
# Won't work
fn pub mut mut_insert(data: T) {
let new_node = Node {
@next = Option.None,
@data = data
}
let old_head = @head := Option.Some(new_node)
new_node.next = old_head
}
I’ll explain why this won’t work shortly in case it isn’t obvious (hint: we’ve seen this problem before). First, notice that we now defined this as fn pub mut instead of fn pub move because we are NOT moving ownership
into this function. Instead, we are giving this function a mutable reference to self. It has to be mutable because we’re going to change the @head variable, and change is a less fancy way of spelling “mutate” (so is mut, apparently).
Next, notice that unlike our previous iteration, this function doesn’t return a LinkedList.
We don’t need to return a new one because we aren’t creating a new one. We’re changing the existing one. I mean, mutating the existing one.
The other thing to notice is that fancy := or “walrus” operator (if you squint, it looks kinda like a walrus’ tusks turned sideways). In Inko, this operator is saying “set @head to the new value and return the old @head.”
Then we use the normal = operator, which is less walrus-y: it assigns that old value of @head that the walrus returned to the variable old_head. Since this equal is lacking a : it isn’t returning anything.
Here’s why this code won’t work:
src/main.inko:37:5 error(moved): 'new_node' can't be used as it has been moved
Move semantics strikes again! When we created the new Option to assign to @head, we gave the Option.Some ownership over the data that used to be in new_node. That means we can’t access new_node anymore.
The solution, in Inko, is to take a mutable reference to new_node before we move it:
let new_node_mut = mut new_node
let old_head = @head := Option.Some(new_node)
new_node_mut.next = old_head
The first line is assigning a mutable reference to the data currently stored in new_node to the variable new_node_mut.
The next line hasn’t changed; we’re moving the data out of new_node into an option.
But the reference we created is still pointing to that data, even though the data itself has been moved. And the reference is mutable,
so we can update the head field to point to the value that was returned by the walrus.
Some languages don’t let you move data while there are mutable references taken out, but it works fine in Inko. The mutable reference
will go out of scope at the end of the function, so it won’t exist anymore, and we know that the underlying owned value will
outlive the reference because it is now owned by @head, which is owned by the linked list, which is living longer than the function
call.
Now this code will work:
class async Main {
fn async main() {
let list = LinkedList.new()
list.mut_insert("hello")
list.mut_insert("world")
}
}
Notice that we didn’t need to make list mut anymore, even though we are later calling a mutable reference method on it. The mut keyword in the previous version
was about changing the list variable, and has nothing to do with the list value. This is pretty normal in object oriented programming, but is different
from most functional languages.
Immutable Reference Functions
We’ve seen move and mutable methods, but we haven’t actually looked at the default way of calling a methods, via immutable receivers. Let’s implement a count method
to show that. This will almost tell us how many elements have been stored in the list, but it doesn’t quite work:
# Doesn't work
fn pub count() -> Int {
let mut count = 0
let mut current = @head
while current.some? {
count += 1
current = current.unwrap.next
}
count
}
First thing to note is that there is no move or mut after fn pub, which means this function accepts self as an immutable reference:
immutablemeans you can’t change any of the fields on self, which means@headwill stay exactly as it isreferencemeans the calling scope still owns the list; we didn’t move it into this method and whatever calls the method will still be able to access the list when this method is complete.
The iteration hopefully isn’t that surprising. We check if the option has a value (that’s what some? does; it returns true if the Option is a Some value rather than None). If it is,
we increment the counter and assign current to its own next field. Then we return the count.
The problem is… this code won’t compile. Notice that:
selfis a reference to a value rather than an owned value- …which means that
@headis a reference to a value rather than an owned value - …which means that
currentis a reference to a value rather than an owned value.
Specifically, current is a ref Option[Node[T]]
The problem is that Option.unwrap is defined in the Inko stdlib as pub fn move. As we now know, move functions takes ownership of its vaule.
We don’t have ownership of the value, so we don’t have the right to pass ownership to unwrap, and we get a compiler error.
The solution is to somehow change our ref Option[Node[T]] to an Option[ref Node[T]].
If we have that, we can unwrap the value because unwrap is now taking ownership of a new owned Option containing a reference to
the original current value, which remains unmodified.
Just change current = current.unwrap.next to current = current.as_ref.unwrap.next and you’re all set.
Most other operations that you might want to perform on a linked list follow a similar structure: you use a loop to perform some operation at each node, then move
the current pointer to the next object. Consider a find method, which returns the position of an element matching a given value:
import std::cmp::(Equal) # Add at the top of the file
fn pub find[U: Equal[T]](value: U) -> Option[Int] {
let mut position = 0
let mut current = @head
while current.some? {
if value == current.as_ref.unwrap.data {
return Option.Some(position)
}
position += 1
current = current.as_ref.unwrap.next
}
return Option.None
}
The body of this method is structurally similar to the count function, but it still has some interesting new concepts. First, notice
that our linked list is behaving like a last-in-first-out (LIFO) stack. So, using this algorithm,
the most recently inserted element will be found at position 0, not the first element we inserted.
So if we call the method like this, the number 1 will be output. world is at position 0 and hello is at position 1:
let list = LinkedList.new()
list.mut_insert("hello")
list.mut_insert("world")
STDOUT.new.print(list.find('hello').unwrap.to_string)
The other interesting bit is the type specialization. Our LinkedList is parameterized to store any type of data, which we specified using
the generic parameter T. The find function doesn’t work on every type of data, though; it only works on data that support the == operator.
So we create a new type parameter named U that is specific to this function, and we specify that the U will only be valid if the LinkedList``'sTparameter implements theEqual` trait.
Of course, this “you have to iterate over the whole list to do anything” pattern is the reason that LinkedLists are rarely used
outside of interview questions and operating system kernels! This obviously means you may want to convert your LinkedList to an array.
The process is similar to the last two methods, with a small twist:
fn pub move to_array() -> Array[T] {
let mut current = @head
let array = []
loop {
match current {
case None -> return array
case Some({@data = data, @next = next_node}) -> {
array.push(data)
current = next_node
}
}
}
}
The key feature here is that we’ve made this fn pub move again. This means that if we ever call list.to_array, we are
moving the list into to_array to be consumed by that function. When we return from to_array, the list is no more.
That’s ok because the thing we are returning is an array that we’ve moved all the values that were previously
in the list into.
I’ve also changed the while current.some? loop to an infinite loop using the loop keyword. Because Inko doesn’t
(currently) allow deconstructing in a let binding, I was going to need a match statement anyway. It felt more elegant
to match on the option than to match on option.unwrap. The loop isn’t really infinite, since we return from it when
we encounter the tail (the node with next=Option.None).
Singly linked lists are pretty simple data structures and I can’t find anything else we can learn about Inko from them, so let’s make things more complicated.
Doubly Linked List
A doubly linked list allocates a bit of extra memory for each node to store a pointer to the “previous” element in the node as well as the “next” one. This adds a very interesting wrinkle to our memory management story:
- Every node has two pointers to it
- Inko is all-in on Single Ownership
- “Single” is emphatically not the name as “Two”
Resolving this dichotomy will help better understand how single ownership works in Inko.
The answer is references. Here’s a first stab at adding a reference to our Node class:
class Node[T] {
let @next: Option[Node[T]]
let @data: T
let @prev: Option[mut Node[T]]
}
The wrapping class, which I’ll call DoublyLinkedList also needs to keep a reference to the tail:
# There's a bug in here that we'll fix shortly
class pub DoublyLinkedList[T] {
let @head: Option[Node[T]]
let @tail: Option[mut Node[T]]
fn pub static new() -> DoublyLinkedList[T] {
DoublyLinkedList {
@head = Option.None,
@tail = Option.None
}
}
}
I wrote this with an intentional memory bug for illustrative purposes. With the following
Main class and function, my code will happily compile:
class async Main {
fn async main() {
let list: DoublyLinkedList[String] = DoublyLinkedList.new()
}
}
Before we continue, I want to add a constructor to the Node class to make the linked list
code a bit more readable. The default constructor will accept data but leave the next and
prev options as None:
fn pub static new(data: T) -> Node[T] {
Node {
@next = Option.None,
@prev = Option.None,
@data = data
}
}
The cool thing about a doubly linked list is that you can push values onto either end of the list.
Let’s start with the push_left function, which is an extended version of insert_mut from the
Single Linked List code:
fn pub mut push_left(data: T) {
let node = Node.new(data)
let node_mut = mut node
match @head := Option.Some(node) {
case None -> {
@tail = Option.Some(node_mut)
}
case Some(old_head) -> {
old_head.prev = Option.Some(node_mut)
node_mut.next = Option.Some(old_head)
}
}
}
We construct a new node that will become the head node, and we take out a mutable reference to that node so we can access it after we move it.
The match statement uses the walrus operator we encountered earlier to assign the new value to @head and deconstruct
the old value. The new value doesn’t have the right next value yet. It’s ok to pass ownership of the new
node to the linked list (via the owned field @head) because we kept a mutable reference to it so we can update
it later.
When the list was previously empty, @head and @tail are both Option.None. In this case, the new head node is actually
already correct because it has no next or previous node, but we need to update the @tail reference to point
to it.
When the list already contains a head, we need to set that old head’s prev reference to the new head node,
which we stored in node_mut. We also need to update the new head’s next variable to take ownership of the
old_head value.
This code compiles cleanly, but if we try to actually use it, the bug I intentionally introduced earlier
will be educational. Update Main as follows:
class async Main {
fn async main() {
let list: DoublyLinkedList[String] = DoublyLinkedList.new()
list.push_left("world")
list.push_left("hello")
}
}
This is good inko code in the sense that it compiles cleanly, but when we run the code, we encounter Inko’s most iconic error:
❯ inko run
Stack trace (the most recent call comes last):
/Code/inko/inko/std/src/std/option.inko:19 in std::option::Option.$dropper
/Code/inko/repro/src/main.inko:4 in main::Node.$dropper
/Code/inko/inko/std/src/std/option.inko:19 in std::option::Option.$dropper
/Code/inko/repro/src/main.inko:4 in main::Node.$dropper
Process 'Main' (0x600002440100) panicked: can't drop a value of type 'Node' as it still has 1 reference(s)
As I’ve mentioned, Inko does its borrow checking at runtime. You would never encounter a runtime error like
this in Rust, for example, because the equivalent Rust code would not compile. However, the equivalent Rust
code is actually rather difficult to write without unsafe because Rust places greater limitations on mutable
pointers: You can only have one mutable pointer at a time and you can’t move a value while it is pointed to.
Working around these limitations results in Rust code that is, yes, safer, but also much harder to read, write,
and maintain than the above. (The normal way to solve a problem like this in Rust is to use RC, which allows for
shared ownership).
As the error message suggests, this error is happening because we still have references to a Node object somewhere
in our code, and when we try to drop the owned value (at the end of main), Inko forbids us from keeping those
owned references around.
Drop Semantics
Earlier I facetiously poo-poo’d the concept of Move Semantics. In Inko, the thing you really need to focus on is “drop semantics.” Drop semantics are all about paying rigorous attention to when references and owned values go out of scope, so you don’t accidentally keep a reference around longer than its owned value, as we did here.
If you have read through Inko’s documentation, you’ll notice small sections called “Drop Semantics” sprinkled throughout the docs. These all explain the order that things are dropped so you can design your code to work with that order.
In our case, the references we are keeping are both fields (@prev and @tail on Node and DoublyLinkedList, respectively).
The drop semantic for fields is to drop them in the order that they are defined, from top to bottom. Consider our current form of
the DoublyLinkedList definition:
class pub DoublyLinkedList[T] {
let @head: Option[Node[T]]
let @tail: Option[mut Node[T]]
}
We defined the owned field @head followed by the mutable reference field @tail. According to the drop semantics,
the @head node will get dropped recursively before the @tail reference. Since the @head node owns a @next node
that owns a @next node that ultimately owns whatever node the @tail reference is pointing to, this means we are
trying to drop the owned tail node before the reference node. The solution is simple:
class pub DoublyLinkedList[T] {
let @tail: Option[mut Node[T]]
let @head: Option[Node[T]]
}
By defining the tail reference before the head reference, we know that the reference will be dropped before the owned data itself is dropped.
This single change is enough to make the code run correctly. But… Why?
Specifically, why does this run correctly, when our Node definition still defines the @prev reference last:
class Node[T] {
let @next: Option[Node[T]]
let @data: T
let @prev: Option[mut Node[T]]
}
For this particular data structure, this code is ok because of the depth-first nature of drops. For any given
node, we drop @next before we drop ourselves. That means that @next.prev will be dropped before ourselves,
and (other than the tail reference), in a properly formatted doubly linked list, self.@next.prev always points to
self. This means that the reference is guaranteed to drop before the thing it refers to, so no error occurs.
That said, I’ve learned in my Inko coding to default to putting references at the top of the list of fields, so I’m going
to change my Node definition as follows:
class Node[T] {
let @prev: Option[mut Node[T]]
let @next: Option[Node[T]]
let @data: T
}
Functionally, it doesn’t make much difference, but its a helpful habit to get into: fields that are (immutable or mutable) references should typically be defined before fields that are owned values.
A Note on Inko’s main drawback
It can be really frustrating to encounter a runtime reference error. Nothing in the error message tells you where the reference that is causing problems lives, and there is very little debugging support. The only information you get is “a reference still exists to this particular value.”
Debugging this reminds me of the first PERL program I ever wrote. The problem wasn’t PERL itself, but that I didn’t
know how to install PERL on my local computer (or even that it was possible). So the only way to debug was to edit
the file, upload it to the cgi-bin/ folder on my webserver via ftp, and then load the page. One of two things
would happen: I would get the output I expected, or I would get “500 Internal Server Error.” That was all the debugging information
available to me (either my host at the time didn’t expose logs or I didn’t know how to access them). My solution
for identifying which line of code caused an error was to comment out half the lines of code and manually bisect
until I found the one that was problematic.
Inko gives me a little more information than that; at least I know which type is causing a reference error, and where in the program the drop is occuring. So I can usually walk the code backwards in my head until I find the extra reference. But there are certainly points where I’ve commented out code to see if it makes the reference error go away.
I don’t think this is specifically a problem with the design of Inko, the language. Rather, it’s part of the current implementation. I imagine tooling in the future that can either do static analysis to detect many of these issues (basically an optional borrow checker) or a debug build that maintains extra information about references at runtime to help identify them.
Inko is a young language. There’s basically no tooling for it other than its own compiler and some syntax files for common editors. The memory management solution it proposes is uncommon enough that new tools and paradigms probably need to be developed to debug it. It’s frustrating to code in this environment unless you’re as weird as I am, in which case it is rather gratifying.
Another aspect of this drawback is that the code inside Inko’s compiler is apparently extremely tricky to get right.
I have encountered no fewer than four different compiler bugs that have caused some variation on these reference
errors that were not the fault of my code. They’ve all been fixed in an amazingly short amount of time,
(I’m in the habit of running off main instead of the release version of inko), so I’m not complaining, but
the process of discovering an error, deciding whether it’s a bug in my code or the compiler, and then constructing
a decent repro and filing a bug report is probably not something a normal person wants to incorporate into their
workflow. (If you aren’t normal, join me in my quest to find every possible Inko bug. It’s fun!)
What about a graph?
Graphs are the canonical data structure for justifying shared ownership and/or garbage collection, especially graphs that can have cycles. I’ve been working on a (currently quite broken) regular expression engine which involves a lot of potentially cyclic finite state machines.
Probably the easiest way to represent a graph in Inko is to create a couple pseudo arenas for the nodes using an array. The array becomes the single owner of all the information in it.
One option for referring to nodes is to store indexes into the array instead of pointers. I’ve seen this model recommended in some articles on memory safety, but I don’t really like it. In my opinion, it’s actually bypassing memory safety. For example, there are no guarantees that an index you have is a legitimate index in the array. Or you might change the value at an index in the array without knowing that a reference to the old data at that index still exists. Assuming your array implementation has bounds checking, this isn’t a security hole like a use-after-free or double-free error, but it is a correctness hole in your program. My take is that if indexing into an array is the best way to solve a memory issue in a “safe” language, it’s because the safety features of that language are not working.
That doesn’t mean you shouldn’t store stuff in an array, though, just that you shouldn’t use array indices as pointers. Because Inko’s pointers are pretty flexible, this isn’t terribly difficult.
Let’s start with a Vertex class that keeps track of its list of sibling nodes in an Array:
class pub Vertex[T] {
let @siblings: Array[mut Vertex[T]]
let @data: T
fn pub static new(data: T) -> Vertex[T] {
Vertex {
@siblings = [],
@data = data
}
}
}
This is a directed and unweighted graph; we aren’t creating a separate Edge class to store weights or other information
on the edge, and there is no requirement that a vertex that has another vertex as sibling must also be a sibling
of that vertex.
I put the @siblings before @data as part of my policy of dropping references first, but it’s not going to matter in
this case since the refrences in the array are never going to be to their own data. At least I hope not. that would
be a terrifying graph. I think an AI could bootstrap itself from that graph.
Note specifically that the Vertex does not own another Vertex. This means that we need to find somebody else to own
the set of vertices in a graph
(I’ve been avoiding writing the plural of “vertex” because all options look wrong, but it seems we’ll be using vertices today).
A new class seems like a reasonable choice:
class pub Graph[T] {
let @vertices: Array[Vertex[T]]
fn pub static new() -> Graph[T] {
Graph {
@vertices = []
}
}
}
One drawback of this design is that nothing at compile time enforces the dependency that “all siblings of a Vertex must
be owned by the same Graph.” so nothing is stopping you from making two graphs and putting the vertices of one graph
as the siblings of another. There may be cases where you think you want to do that, but think for a moment about drop
semantics: What happens when you drop a graph that has references to it from another graph? Answer: the same thing
that happens when you drop anything that has references between them: a runtime error that is, as we’ve discussed, pretty hard to debug.
Adding data to this graph is a straightforward method on the Graph class:
fn pub mut add(data: T) -> mut Vertex[T] {
let vertex = Vertex.new(data)
let vertex_mut = mut vertex
@vertices.push(vertex)
return vertex_mut
}
We need to mutate the vertices field, which means we need to accept self as a mutable receiver. We return a mutable reference
to the node that was created so that the consumer can do things with it. Since we need the reference after it is moved
into the array, we construct the reference in advance.
This creates a disconnected graph and there’s not yet any way to connect edges. We can resolve
that with a add_edge method on the Vertex class:
fn pub mut add_edge(vertex: mut Vertex[T]) {
@siblings.push(vertex)
}
With these two methods we can start constructing a graph in our main function:
class async Main {
fn async main() {
let graph: Graph[String] = Graph.new
let hello_mut = graph.add_node("Hello")
let world_mut = graph.add_node("World")
let kitty_mut = graph.add_node("Kitty")
hello_mut.add_edge(world_mut)
hello_mut.add_edge(kitty_mut)
}
}
Now is a good time to talk about drop semantics within a method. Recall that the drop semantics for fields on a class are to
drop them in the order they are defined. So, for our Node class, @siblings is dropped before @data because that’s the
order we defined them.
Within a method, local variables are dropped in reverse, from the last one defined until the first one defined. So for the main method above,
we first drop kitty_mut, then world_mut, then hello_mut, and finally graph. Since all the owned variables are in the graph
and we’re dropping the outside references before we drop the graph, we know that the *_mut references are not outliving
the nodes in the graph.
Unfortunately, this isn’t enough. the *_mut references aren’t the only references we have hanging around. Try adding one more line
to the main method:
kitty_mut.add_edge(hello_mut)
This is introducing a cycle in the graph. Cycles can be annoying to work with in general, but there are real-world problems that rely on them, so we need to make sure our code supports those cycles. Sadly, it doesn’t:
❯ inko run
Stack trace (the most recent call comes last):
/Code/inko/repro/src/main.inko:45 in main::Main.main
/Code/inko/repro/src/main.inko:20 in main::Graph.$dropper
/Code/inko/inko/std/src/std/array.inko:91 in std::array::Array.$dropper
/Code/inko/inko/std/src/std/array.inko:485 in std::array::Array.drop
/Code/inko/repro/src/main.inko:4 in main::Vertex.$dropper
Process 'Main' (0x600003380100) panicked: can't drop a value of type 'Vertex' as it still has 1 reference(s)`
We can’t drop the hello node first because kitty’s @siblings contains a reference to it. But we can’t drop
kitty first either, because hello’s @siblings array contains a reference to it. Whatever shall we do?
Well, we know we need to be able to drop all the references before we start dropping any of the owned nodes. Inko doesn’t implicitly support this, so we’ll have to give it a hint:
import std::drop::(Drop) # At top of file
impl Drop for Graph { # Somewhere after the graph class
fn mut drop() {
@vertices.iter_mut.each fn (vertex) {
vertex.siblings.clear
}
}
}
The first line imports the Drop trait. A trait is a sort of compile-time interface that you can have your
classes opt to implement. The Drop trait, specifically, features a single method drop, which
accepts self as a mutable receiver with no arguments.
Inko’s runtime will call the drop method on a class just before that object goes out of scope. The drop method
is responsible for performing any “cleanup” operations that either:
- prevent the object from being dropped cleanly, as we are doing here
- would leave resources lying around such as closing a socket or file
Our drop code above is iterating over all the vertices in the graph. We use iter_mut instead of iter so we get
a mutable reference to each vertex. We need this so we can mutate the siblings array, namely by calling the mut clear
method on it.
Once this drop method exits, there will be no references to any vertex from any other vertex in the graph.
That means that it is safe for Inko’s runtime to drop each of the nodes in the @vertices array
so the code will now run cleanly without that pesky reference error.
The problems with Drop
The Drop trait has some severe limitations that tend to make me avoid using it if I can get around it:
- It is impossible to deconstruct a class that has a custom
dropmethod. For theGraphexample, you can no longer ever writematch graph {case {@vertices=vertices} -> ...}to move theverticesarray out of thegraphIn practice, this means you will tend to want to put the customdropmethods on “high level” classes such asGraphthat you are less likely to want to deconstruct. If you design your code such that you need a custom drop onVertex, for example, you would likely discover that complex algorithms (dijkstra’s, anyone?) are difficult because you can’t match on the contents of the nodes. (One way around this is to match on references to nodes instead, but that isn’t always what you want to do) - You can’t move a field out of self in a moving method if
selfhas a customdropmethod. So if we wanted to create apub move partitions() -> Array[Graph]function on theGraphclass, we would not be able to move the@verticesarray out of the graph inside that function. Luckily, that wouldn’t be necessary for identifying partitions in a graph, but it can still lead to problems.
I’ve been bitten by these a few times, so I try to structure my code such that custom drop implementations
are not necessary whenever I can. I haven’t actually had to define one yet, and the graph example above
is probably the first place that I’ve felt I had a legitimate reason to do so.
Another Take on Graph Ownership
Graphs are extremely generic data structures, to the point that it barely even makes sense to implement one without knowing what it’s going to be used for. Data structures such as linked lists and all kinds of trees are just graphs with restrictions, after all.
Depending how your graph is going to be structured, it may make sense to have one adjacent node own another. For example, in a filesystem, the “root” directory contains other directories, so it might be reasonable to have the root directory own it.
Another example is nondetermisitic finite state automata, which are the key data structure in a regular expression parser. I’ve learned a lot about these recently as I’ve been exploring writing a regex parser in Inko. I am toying with writing an article on the topic, but for now I’ll point you to the one I’ve found most useful as a reference: https://deniskyashif.com/2019/02/17/implementing-a-regular-expression-engine/.
Some attributes I’ve relied on when modelling a regular expression include:
- They have a definite start and end state
- Any node must have a directed edge to at least one other node
- Any node can have at most two edges directed to other nodes
- Edges are directed, but not acyclic, meaning nodes can point back to some node that is closer to the start than itself
Note: I’m not 100% certain if the third point (maximum of two other nodes) is a proven property of regular expressions or is just a property of the ones I’ve been modelling so far.
I don’t think there is a limit on how many edges can point to a single node from other nodes.
These properties, combined with the way that regular expression NFAs are constructed, actually make it pretty easy to define an ownership model for them:
- The start node (transitively) owns all the nodes in the NFA.
- Any node that is connected to exactly one other node owns the other node it is connected to.
- Any node that is connected to two nodes will own at least one of the nodes it is connected to.
- A node that is connected to two nodes may have a reference to another node.
For example, one of the more complicated regular expressions is the closure (zero or more), which is modelled something like this:
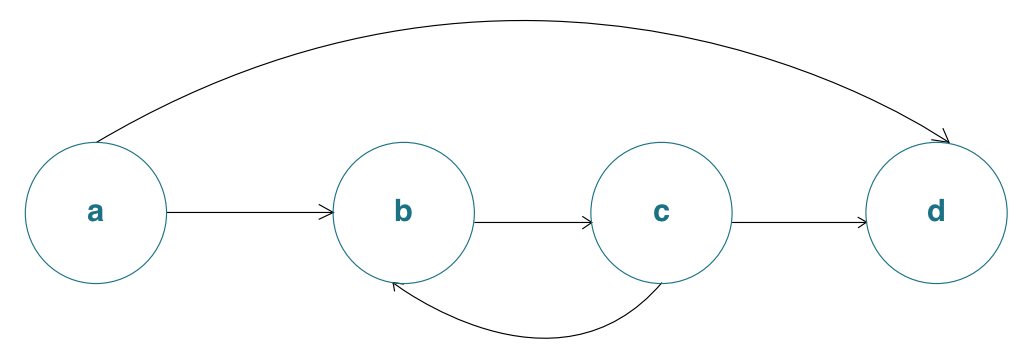
The letters are meaningless; I just assigned them so we can understand which node we’re talking about throughout the text. In a regex parser, the characters being matched don’t actually go on the nodes; they go on the edges. For this example, I’ve left symbols off the edges since we’re more interested in the ownership semantics of the underlying structure of this NFA than the acual regularness of the expressionies.
Since b is the only node that points to c, we know that b has to own c. The straight line of consecutive arrows
across the middle suggests that a should own b and c should own d as well.
However, an alternative would be for a to own d and c to own b. This might be reasonable depending on how the NFA has
been built up from the smaller NFAs that comprise it. It doesn’t matter too much as long as we are clear that nodes b and d
each have two arrows pointing to them. Only one of each of those arrows can own the pointed-to-node, so the other one
clearly has to be a reference.
The question is, how can we model these edges such that sometimes there is one owned edge, sometimes there are two, and sometimes there is a reference edge?
In Inko, we can elegantly model this structure using algebraic data types, or enum classes. ADTs allow us to
define that a class can be one of several given structures. Start with a Transition enum class like this:
class pub enum Transition {
case End
case Owned(Node)
case Ref(mut Node)
case Split(Transition, Transition)
}
Note that there are two way to reference a single node. The Owned case takes ownership and the Ref case takes
a mutable reference. This is able to model all of the arrows in the diagram. The circles we can model with a new (normal) Node class:
class pub Node {
let @transition: Transition
}
Node has only one field, a transition, which it owns. The transition has the useful property of being able
to be any of the four possible transition cases defined above.
Let’s add a constructor method to Node to make it a little easier to construct a Node, given a transition:
fn pub static new(transition: Transition) -> Node {
Node {
@transition = transition
}
}
Nothing new here; we take ownership of the transition passed in and construct a new Node, wrapping that argument.
In order to safely construct our closure NFA, we need to be able to replace the transition on a Node. This will allow us to
create a Node with the “wrong” transition and then grab a mutable reference to that Node so we can construct
other transitions. This will make sense shortly; for now, here’s the replace method:
fn pub mut replace(transition: Transition) -> Transition {
@transition := transition
}
Note the walrus operator; this is moving the new transition into @transition and returning whatever the old transition
was, in case it is useful.
Now comes the hard part: We want to construct the above graph in our main function. I’m going to do this incorrectly
several times so you can see all the little gotchas you need to watch out for when writing Inko code.
Start by creating the Main class and main method, and construct exactly one node, the d node. d is unique because
it doesn’t transition to any other nodes, so we construct it with a Transition.End:
class async Main {
fn pub async main() {
let d = Node.new(Transition.End)
}
}
I’ve decided that c is going to own d, rather than having a own d. But I can’t construct c yet because I need
a reference to b to do so. Yet I can’t construct b either because it needs to own c. We can solve this chicken
and egg problem by constructing c with a Transition.End as well. We’ll be throwing away that Transition.End eventually,
but it’ll be enough to give us a c that b can own:
class async Main {
fn pub async main() {
let d = Node.new(Transition.End)
let c = Node.new(Transition.End)
let b = Node.new(Transition.Owned(c))
}
}
Now that we have a b, we can update the c node to hold its split transition. But wait! We actually can’t update c because
we’ve already moved it into b. Try this code, for example:
class async Main {
fn pub async main() {
let d = Node.new(Transition.End)
let c = Node.new(Transition.End)
let b = Node.new(Transition.Owned(c))
c.replace(Transition.End) # compiler error
}
}
This will throw a compiler error:
src/main.inko:29:5 error(moved): 'c' can't be used as it has been moved
The solution is to take out a mutable reference to c before we move it into b. Then we can update the reference after b
exists:
class async Main {
fn pub async main() {
let d = Node.new(Transition.End)
let c = Node.new(Transition.End)
let c_mut = mut c
let b = Node.new(Transition.Owned(c))
c_mut.replace(Transition.Split(
Transition.Owned(d),
Transition.Ref(b),
))
}
}
The new lines replace the Transition.End that we originally put into c with a Transition.Split that holds two other
transitions: An owend transition to d and a reference transition back to b. Note that we didn’t need to pass mut b
into Transition.Ref because Inko knows that Ref holds a mut Node, so it automatically passes a reference instead
of moving b.
This code compiles, but it doesn’t run correctly. It gives us the dreaded still has 1 reference error. The problem
is that local variables are dropped in the reverse order that they are defined. In this code, that means that b gets
dropped first, since it is the last one defined. But b contains an owned transition to c, so the first step of
dropping b is to recursively drop c. But we can’t drop c because the c_mut reference has not been dropped yet.
This particular case doesn’t actually happen in my real regular expression code because the nodes are constructed in method calls so temporary references like that go out of scope in the method call while the owned value outlives them. Luckily, we did encounter it here so I can show you a useful/weird trick with scopes:
class async Main {
fn pub async main() {
let d = Node.new(Transition.End)
let c = Node.new(Transition.End)
let b = Node.new(Transition.End)
{
let c_mut = mut c
b.replace(Transition.Owned(c))
c_mut.replace(Transition.Split(
Transition.Owned(d),
Transition.Ref(b),
))
}
}
}
Here I’ve wrapped the c_mut code in curly braces to define a new scope. Any variables defined inside the new curly
braces are dropped at the end of the curly brace; in this case, that means c_mut. I moved the definition of b
outside the curly braces, and made it point to a Transition.End that I’m going to discard right away. Then
after I take out c_mut I can use replace to replace b’s transition with the real one.
We’re almost done. Now we need to define the a node, which needs to take ownership of b and also hold
a reference to d. This ends up changing the code quite a bit, but it’s reusing the same concepts:
class async Main {
fn pub async main() {
let a = Node.new(Transition.End)
let d = Node.new(Transition.End)
let d_mut = mut d
let c = Node.new(Transition.End)
let c_mut = mut c
let b = Node.new(Transition.Owned(c))
c_mut.replace(Transition.Split(
Transition.Owned(d),
Transition.Ref(b),
))
a.replace(Transition.Split(
Transition.Owned(b),
Transition.Ref(d_mut)
))
}
}
In the end, the only node that needs to outlive the references is a because a ultimately takes transitive ownership of all
the other nodes. We don’t need to put the two variables d_mut and c_mut inside a scope anymore because they are defined
after a, so that they do not outlive it.
We don’t need the fake Transition.End on b anymore so I changed that back to Node.new. Finally, I created
a new Transition.Split for a so that it can take ownership of b and hold a reference to d.
This compiles correctly, but once again (because I wrote this code wrong for pedagogical purposes), we get the
dreaded still has one reference error. This is where we need to understand drop semantics on enum classes.
If any given case contains more than one element (such as Transition.Split, in this case—literally), they
are dropped in order from left to write.
In the above code, we are defining two Transition.Split elements, and both of them are putting their Transition.Owned
before their Transition.Ref, which means owned stuff is getting dropped while references still exist. Switching
them up makes the error go away:
class async Main {
fn pub async main() {
let a = Node.new(Transition.End)
let d = Node.new(Transition.End)
let d_mut = mut d
let c = Node.new(Transition.End)
let c_mut = mut c
let b = Node.new(Transition.Owned(c))
c_mut.replace(Transition.Split(
Transition.Ref(b),
Transition.Owned(d)
))
a.replace(Transition.Split(
Transition.Ref(d_mut),
Transition.Owned(b)
))
}
}
I should note that this model is a lot simpler than the one I’m using in my regex library, and my code relies on the fact that regular expressions are built up from smaller pieces. But it does give a little more insight into how you need to think about single ownership to code effectively in Inko. It’s taken me a lot of trial and error to figure out some of these techniques, and I felt that collecting them together would be a good way to contribute back to the Inko community.
This was a pretty epic post so I’m going to stop here. Next up, I have more thoughts on Inko lined up, and will either be talking about unique pointers and concurrency or possibly a deep dive into regular expression parsing (if I ever figure it out…).